每種物質都是由原子和分子組成。根據定義,物質的量以摩 爾表示。 一摩爾的物質含有 6.022 · 1023 個構成粒子 (阿伏 伽德羅常數。這不是無量綱數值,而是具有單位 mol-1 的物 理量)。1 摩爾的定義是 系統物質的量,其包含的粒子數目 與 12 g 碳同位素 12C 中所含的原子數目完全相同。
在標準狀態下,即壓力為 101.325 Pa 且溫度為 273.15 K (0°C),一摩爾理想氣體填充的體積為 22.414 升。
早在 1664 年,羅伯特·波義耳就研究壓力對一定量空氣的影 響規律,被馬略特在實驗中證實。研究結果在波-馬定律中表 述為:
![]()
公式 1-4: 波義耳定律
用文字表述波-馬定律:一定質量的氣體,在溫度不變的情況 下,其壓力與體積成反比—壓力與體積的乘積恒定不變。
百余年后,一定量的氣體,其體積與溫度的關系也表述為: 一定量的氣體,在壓力不變的情況下,其體積與絕對溫度成 正比,即
![]()
公式 1-5: 蓋-呂薩克定律
一定量的氣體受壓力變化和溫度變化影響的結果是
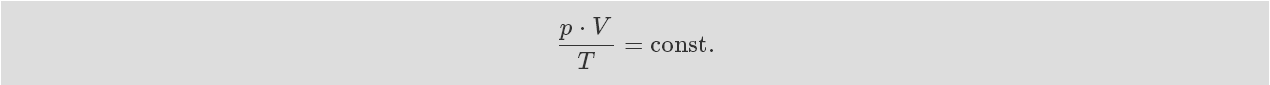
這仍適用于一定量的氣體。一定溫度和一定壓力下的氣體體 積與物質的量成正比。我們因此可以這樣書寫:
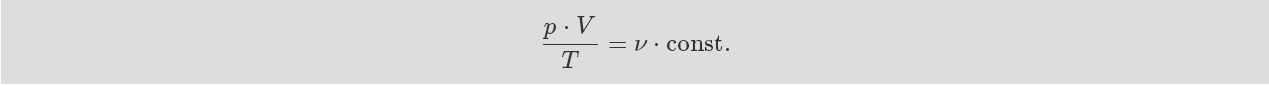
物質的量可以通過稱重來確定。我們可以通過質量與摩爾質 量之比來表示氣體的量。 常數const. 在方程中對應是 1 摩爾 氣體,并且它被稱為氣體常數 R。 因此,理想氣體狀態 可描述為如下的壓力、溫度和體積的函數關系:
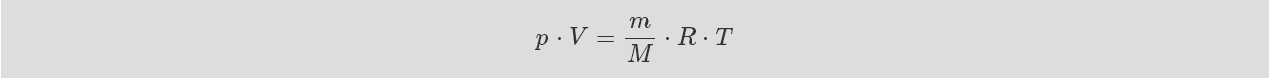
公式 1-6: 理想氣體狀態一般方程
| P | 壓力 | [Pa] |
| V | 體積 | [m3] |
| M | 質量 | [kg] |
| 摩爾質量 | [kg kmol-1] | |
| R | 一般氣體常數 | [kJ kmol-1 K-1] |
| T | 絕對溫度 | [K] |
物質的量也可表示為與阿伏伽德羅常數對應的分子數。
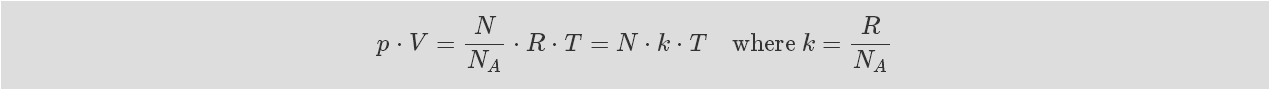
公式 1-7: 理想氣體狀態方程 I
| N | 粒子數目 | ||
| Na | 阿伏伽德羅常數 | = 6.022 · 1023 | [mol-1] |
| K | 波爾茲曼常數 | = 1.381 · 10-23 | [J K-1] |
如果等式兩邊同時除以體積,則我們得到
![]()
公式 1-8: 理想氣體狀態方程 II
N粒子 數密度[m-3]




 售前客服
售前客服